Impermanent Loss

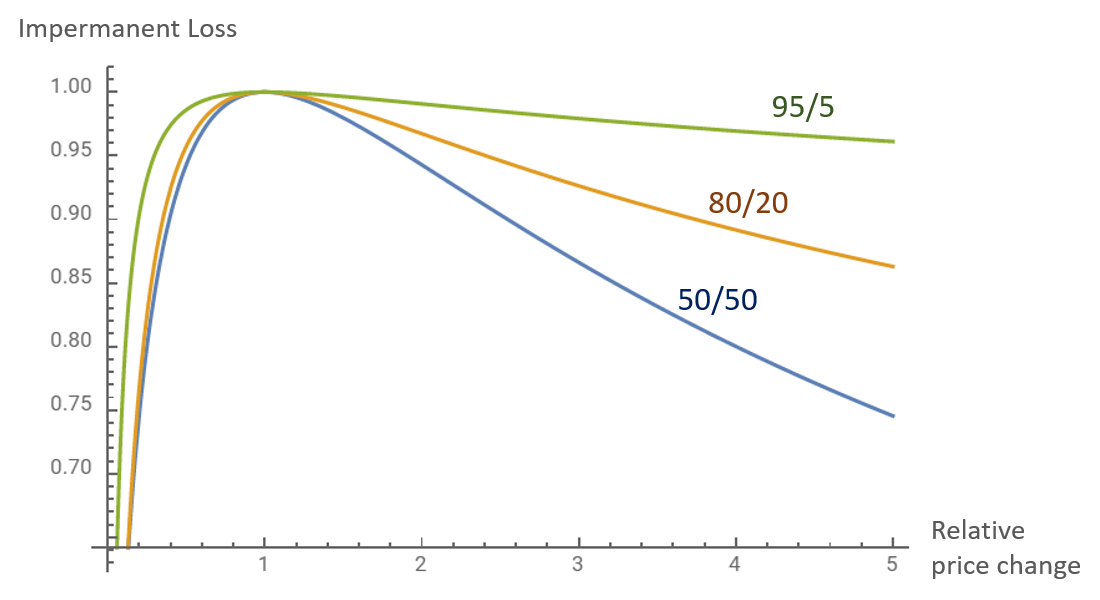
Impermanent Loss, sometimes referred to as divergent loss, can simply be put as the opportunity cost of adding liquidity into an AMM pool vs holding the individual tokens.

Impermanent loss occurs when the prices of two assets experience a divergence in price action. For example if two assets increase by 20% no impermanent loss is noticed; however, if one asset increases in value by 20% then a divergence has taken place and some form of impermanent loss would be noticed in the position. This can be reversed by the other token in the pool also increasing 20% or both tokens converging on the same price movement relative to the original amount the user put in the pool. A basic example of impermanent loss followed by reversal scenario are is outlined on the following page.

$IL ={\frac {PoolValue}{HodlValue}}-1$

Impermanent Loss - Relationship shown based on a two token pool with one asset and one stable coin.

::: tabs

@tab 50/50 Pools

50/50 Pools

We will start with a simple 50/50 pool featuring COMP/WETH. We take a time when WETH is worth $2,000 USD and we have 2.5 WETH ($ 5,000.00). At the same time COMP is worth $250.00; therefore, the corresponding amount is 20 COMP tokens. Our liquidity position is deposited and we receive pool tokens for this$ 10,000 join.

We check back out our position after a period of time and COMP has doubled, 100% gains straight to $500.00 USD. WETH has only made it up to$ 2300.00 at this point, gains of just 15%. We know at this point we will face some impermanent loss. We still have strictly gains but due to our liquidity position we are missing out on some of the theoretical gains.

Here we calculate the invariant from the value function:

$V= \prod_t B_t^{W_t} \\\$

B_{i-WETH} = 2.5 \ W_{i-WETH}=0.5 $$ $$ B_{i-COMP} = 20 \ W_{i-COMP}=0.5 \\

$Initial \ Invariant: V = B_{i-WETH}^{W_{i-WETH}} * B_{i-COMP}^{W_{i-COMP}} \\$ $V = 2.5^{0.5} * 20^{0.5} = 7.0710678 \\$

After \ Arbitrage: 2.5 \ WETH \ and \ 20 \ COMP \ yields: $$ $$(2.5*1.15)^{0.5} * (20*2)^{0.5} = 10.723805

Our gains will be determined by the invariant ratio, this value can be used for our token balances as well.

$Invariant \ Ratio_{LP} = {\frac{10.723805}{7.0710678}} = 1.51657509$ $Ratio_{HODL} = (1.15*0.5) + (2*0.5) = 1.575$

Here we can consider the USD values to be the same in the numerator and denominator therefore not needed to determine the ratio between the two. $$IL = {\frac{Invariant \ Ratio_{LP}}{Ratio_{HODL}}} = {\frac{1.51657509}{1.575}} - 1 = -0.03709518$$ $$ IL = -3.709518\%$$

For the new token balances we consider the invariant ratio compared to the price action of the individual asset. This proportion will yield the new balance of each token in relation to the initial join amount.

$New \ Token \ Balance: B_{t'}= B_{t} *{\frac{Ratio_{LP}}{Price \ Action_{t}}}$ $WETH: 2.5 * {\frac{1.5657509}{1.15}} = 3.2969$ $COMP: 20 * {\frac{1.5657509}{2}} = 15.1657509$

_**Please note these calculations can take place over any time frame. These occurred in roughly 12 days between June 25 and July 07 of 2021. This same price action can take place over the course of 1 year and with 4% or more in swap fees or liquidity mining accumulating the LP position would become the more attractive option.**_ These calculations are depicted by the following tables. **Initial Liquidity Position Amount: $10,000.00** $$ \begin{array} {|r|r|}\hline Token & Initial \ Value($) & Balance & USD \ Amount & Weight \\ \hline WETH & 2000 & 2.5 & 5000 & 0.5 \\ \hline COMP & 250 & 20 & 5000 & 0.5 \\ \hline \end{array} $$ **HODL Total: $15750.00** $$ \begin{array} {|r|r|}\hline Token & Initial \ Value($) & Balance & USD \ Amount & Weight \\ \hline WETH & 2300 & 2.5 & 5750 & 0.5 \\ \hline COMP & 500 & 20 & 10000 & 0.5 \\ \hline \end{array} $$ **LP Total $15165.75; with 4% Annual yield $15,772.38** $$ \begin{array} {|r|r|}\hline Token & Initial \ Value($) & Balance & USD \ Amount & Weight \\ \hline WETH & 2300 & 3.2969 & 7582.87 & 0.5 \\ \hline COMP & 500 & 15.16575 & 7582.87545 & 0.5 \\ \hline \end{array} $$ In our prior example COMP and WETH went through divergent price changes. When this happens, we saw the potential loss of value that can be created by the nature of impermanent loss. Now if our prices continue to change, we will look at an example where WETH goes up to a price of $3000.00 and COMP decreases down to $375.00. While these are diverging prices changes this will bring us to a 50% gain for both assets in relation to our original Liquidity Position. $$ V=20^{0.5}*2.5^{0.5}=7.071068 $$ $$ V_2= (20*1.5)^{0.5}*(2.5*1.5)^{0.5}=10.6066017 $$ $$ Invariant\ Ratio= {\frac {V_2}{V}}={\frac {10.6066017}{7.071068}}=1.5 $$

Therefore, because our invariant ratio matches our price action ratio, we have an indicator that there will be no impermanent loss.

$IL = {\frac{Invariant \ Ratio_{LP}}{Ratio_{HOD}}} = {\frac{1.5}{1.5}} - 1 = 0 \ or \ 0.00\%$

This calculation will be done from the point where impermanent loss was experienced to the current state to prove the “loss” is indeed reversible under the proper conditions. **Initially:** $$ 3.2969 \ WETH \ at \ 2300.00 \ each \ and \ 15.16575 \ COMP \ at \ 500.00 \ each $$ $$ V = 15.16575^{0.5}* 3.2969^{0.5} = 7.071068 $$ **After Price Change:** $$ V_{2} = (15.6575 * 0.75)^{0.5} * (3.2969 * 1.30435)^{0.5} = 6.9937835 $$ $$ Invariant \ Ratio = {\frac{V_{2}}{V}} = {\frac{6.99378335}{7.071068}} = 0.9890703 $$

New Token Balances can be calculated as follows:

$New\ Token\ Balances:B_{t'}*{\frac {Ratio_{LP}}{Price\ Action_t}}$ $WETH:3.2969*{\frac {0.9890703}{1.30435}}=2.5$ $COMP: 15.16575*{\frac {0.9890703}{0.75}}=20$

<!-- prettier-ignore-end --> These balances match our initial liquidity position meaning overall we lost nothing impermanent loss. The price action is still in our favor by 50% for both assets as we hold the same initial number of each. Also, we would have likely collected swap fees for this from swappers making our gains slightly larger. Through the price action regardless of how dramatic impermanent loss can be reversed as seen above. This can occur countless times as prices of assets in a pool fluctuate in price. The importance of this is understanding the assets you are holding and how comfortable you are with volatility. In theory great volatility will be coupled with large swap volumes, making the swap fees and gains for liquidity providers increase. Weighing the risk of impermanent loss with the accumulation of swap fees or “volatility farming” is the game of a liquidity provider long term. @tab 80/20 Pools # 80/20 Pools Here we will examine the same circumstance as shown in the 50/50 Pools example to compare what effect a change in pool weights can have on a liquidity provider's position. <!-- prettier-ignore-start --> #### COMP WETH 80/20 To emphasize the weighting of 80 / 20 as opposed to 50/50 we will observe impermanent loss under the COMP favoring pool conditions to display the benefits of uneven pool weightings. We will in turn hold 1 WETH @ $2000.00 each and 32 COMP @ $250.00 each. ($8000 in COMP and $2000 in WETH). $$ B_{i-WETH} = 1 \ \ W_{i-WETH} = 0.2 $$ $$ B_{i-COMP}= 32 \ \ W_{i-COMP} = 0.8 $$

$Initial \ Invariant \ = 1^{0.2} * 32^{0.8} = 16.00$ $After \ Arbitrage: \ 1 \ WETH \ and \ 32 \ COMP \ yields:$ $(1*1.15)^{0.2} * (32 * 2)^{0.8} = 28.647290182$

Our gains will then be determined by the invariant ratio. This can be used for our token balances as well. $$ Invariant \ Ratio_{LP} = {\frac{28.647290182}{16}} = 1.7904556364 $$ $$ Ratio_{HODL} = (1.15 * 0.2) + (2 * 0.8) = 1.83 $$

Here we can consider the USD values to be the same in the numerator and denominator therefore not needed to determine the ratio between the two. $IL = {\frac{Invariant \ Ratio_{LP}}{Ratio_{HODL}}} = {\frac{1.17904556364}{1.83}} = -0.02160893 \ or \ 2.160894\%$

While impermanent loss is still applicable in this scenario in comparison to the 50/50 pool the losses are nearly cut in half (a factor of 0.5825 more precisely). When dealing with very large liquidity positions these small amounts can make a large difference in value and ultimately weighting will protect or expose liquidity providers from impermanent loss depending on their choices; however, if prices return to their initial state or follow the same price change at a certain point the “losses” will revert to zero regardless of weighting. <!-- prettier-ignore-end --> @tab Multi-token Pools # Multi-token Pools Balancer's multi-token pools are on of our unique features. Below is an example of how impermanent loss on one of these pools on the can occur. Inclusive of details on volatility and stable coins. #### Advanced Example – Multi Token Pool An example of a multi token pool and how impermanent loss would occur and then be reverted will be solved below. We will look at a Polygon pool: 25% USDC, 25% WMATIC, 25% BAL, 25% WETH. Initially we will assume we joined with $10,000 in USD evenly amongst the assets. <!-- prettier-ignore-start --> ##### Initial Conditions: $$ USDC \ at \ $1.00 = 2500 \ USDC \ \ \ WMATIC \ at \ $1.25 = 2000 \ WMATIC $$ $$ BAL \ at \ $25.00 = 100 BAL \ \ \ WETH \ at \ $2500.00 = 1.0 \ WETH $$

We will assume USDC stays at a constant value, BAL increase by 15% to $28.75, WMATIC decreases 4% to$ 1.20, and WETH increase 50% to $3750.00. $V_{initial} = 2500^{0.25} * 2000^{0.25} * 100^{0.25} * 1^{0.25} = 149.534878$ $V_{2} = (2500)^{0.25} * (2000 * 0.96)^{0.25} * (100 * 1.15)^{0.25} * (1 * 1.5)^{0.25} = 169.631923$

Invariant \ Ratio = {\frac{V_{2}}{V_{initial}}} = {\frac{169.31923}{149.534878}} = 1.13439704 $$ $$ Ratio_{HODL} = (1 * 0.25) + (0.96 * 0.25) + (1.15 * 0.25) + (1.5 * 0.25) = 1.1525

$IL = {\frac{Invariant \ Ratio_{LP}}{Ratio_{HODL}}} = {\frac{1.13439704}{1.1525}} - 1 = 0.0157076 \ or \ 1.57076\%$

New Token Balances can be calculated as follows:

$New \ Token \ Balances \ B_{t'} = B_{t} * {\frac{Ratio_{LP}}{Price \ Action_{t}}}$

$$ USDC = 2500 * {\frac{1.13439704}{1}} = 2836 \ USDC $$ $$ WMATIC = 2000 * {\frac{1.13439704}{0.96}} = 2363.327 \ WMATIC $$ $$ BAL = 100 * {\frac{1.13439704}{1.15}} = 98.643 \ BAL $$ $$ WMATIC = 1 * {\frac{1.13439704}{1.5}} = 0.7562647 \ WETH $$ Due to a stable coin (USDC) being a portion of the pool, impermanent loss is nearly inevitable unless all tokens return to their initial value at the time of liquidity provision; therefore, the pool above and any pool with stables and non-stable assets a Liquidity Provider is concerned mostly with volatility and their profit to be made from swap fees or liquidity mining. They are essentially positioning themselves with the expectations of this type of price pattern: ![Price Chart for mid-July 2022 COMP](/images/Multi-token-chart.png) ##### One may provide liquidity to a pool in whch USDC and an asset (X) at 14.01 are present in mid-July. Then by the time the chart comes to an end the price is still 14.01 after going through stages of upward and downward price changes. This will yield an amount of swap fees to be collected as profit as well as 0% impermanent loss. At any point where all prices revert to their initial values, arbitragers will bring the tokens back to their initial balances. With a stable token present this would mean no gains can be made without impermanent loss or swap fees being present. In turn the goal can be considered to have low IL and high swap or liquidity mining for a liquidity provider with these types of positions. Also, it can be viewed to manage exposure to volatile assets.

$V_{current} = 2836^{0.25} * 2363.327^{0.25} * 98.643^{0.25} * 0.7562647^{0.25} = 149.53489$ $V_{2}= (2836)^{0.25} * (2363.327 * 1.04167)^{0.25} * (98.643 * 0.8696)^{0.25} *$ $(0.7562647 * 0.67)^{0.25} = 131.8204$ $The \ values \ above \ were \ shortened \ for \ formatting$

{\frac{131.8204}{149.53489}} = 0.881536 \ The \ calculations \ below \ will \ yield \ the \ $$ $$ initial \ token \ balances \ therefore \ IL = 0\%

$USDC = 2836 * {\frac{0.881536}{1}} = 2500 \ USDC$ $WMATIC = 2363.327 * {\frac{0.881536}{1.04167}} = 2000 \ WMATIC$ $BAL = 98.643 * {\frac{0.881536}{0.8696}} = 100 \ BAL$ $WETH = 0.7562647 * {\frac{0.881536}{0.6667}} = 1 \ WETH$

:::

Overview Preminted Bpt